  |
 |
|
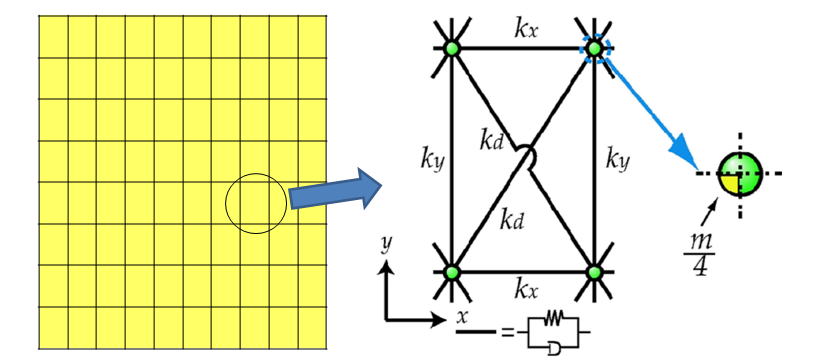
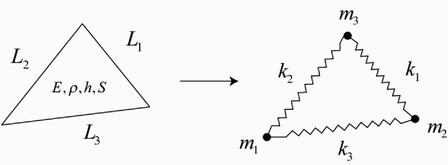
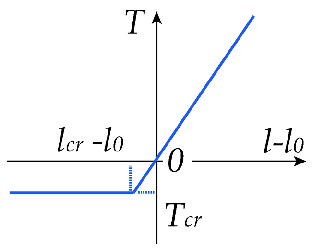
| 図1. 四角形要素 | 図2. 三角形要素 | 図3. ばねの復元力特性 |
 |
 |
| 収納時 | 展開時および拡大図 |
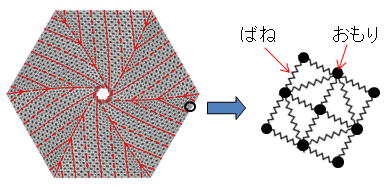
| 図3. らせん折り膜面多粒子系モデル | |
 |
 |
| (a) 実験 | (b) 数値シミュレーション |
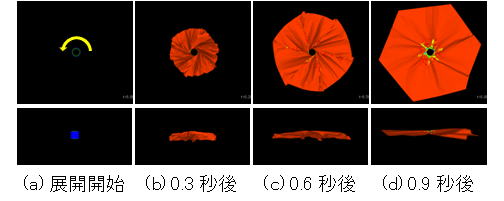
| 図4. 展開形状の比較 | |
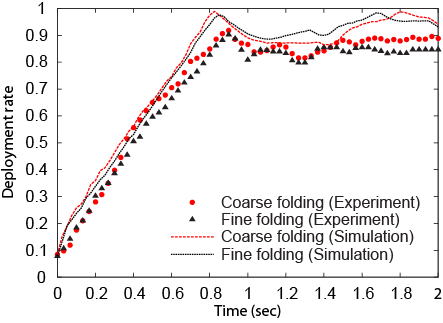 |
| 図5. 展開率の比較 |
概要
ソーラーセイルや大型展開アンテナ,宇宙太陽発電システムなどの今後の大型宇宙構造物は,ロケットの打ち上げ能力の制約のため,軽量で折り畳みが可能な膜面を利用して構築することが必要であると考えられている.しかし,高真空かつ無重力を模擬した大きな環境を地上で実現することは極めて困難なため,宇宙での大型柔軟膜面構造物の挙動を把握するためには,数値シミュレーションによる検討が必須となる.宇宙構造物に使用される膜面は,厚さ数ミクロンと非常に薄く,柔軟に変形し,容易に座屈する.また,折り畳みによって生じる折り癖を考慮する必要合もあり,効率良く高精度な数値シミュレーションを行うには様々な工夫が必要である.そのため,非線形FEMの他に,膜面を多数のばねと質点のネットワークでモデル化し,比較的高速なシミュレーションが可能な多粒子系モデルが考案された.この解析法は,最近CGや流体シミュレーションなどの分野で研究されている粒子法の一種と考えられる.
本研究では,多粒子系モデルに座屈強度や折り癖などのモデルを導入して改良を行い,実験結果と比較して有効性を検証している.
多粒子系モデル
膜面の多粒子系モデルは,基本的には膜の曲げ剛性を無視して面内剛性と密度をばね・質点系でモデル化したもので,四角形要素(図1)と三角形要素(図2)が開発されている.四角形要素は,膜面を四角形格子に分割し,各格子点に質点を,四角形の辺と対角線にばねを配置したもので,質点の質量は四角形要素の質量の1/4とし,ばね剛性は,一要素における荷重と変位の関係と,等方弾性体における応力とひずみの関係から得られる荷重と変位の関係とが等しくなるように決定する.三角形要素は,図2の左図のように三角形膜要素を右のばね・質点系に置き換えるもので,任意の膜面形状に対応できるため有利である.図2において,質点の質量miは,膜面の質量ρhSの1/3とする.ばね定数kiは,各辺に平行な3通りの一軸引張状態における膜の歪みエネルギーとばねに蓄えられるエネルギーとが一致するように定める.隣り合う三角形要素の質量とばね剛性を重ね合わせることにより,膜面全体の多粒子系モデルを構築する.どちらの要素においても,膜面の座屈を考慮し,図3のように圧縮時のばねの復元力またはばね剛性を微小にすることが重要である.lはばねの長さ,l0は自然長,lcrは臨界長さ,Tは張力,Tcrは臨界座屈強度である.
以下の例では,基本的な三角形要素を元に,座屈,折り目剛性,減衰,空気抵抗のモデル化を改良,追加して用いている.折り目剛性のモデル化は本研究で新規に導入したものである.
(詳細は参考文献を参照のこと).
らせん折り膜面の遠心力展開ダイナミクス
図3が三角形要素でモデル化したらせん折り膜面の遠心力展開実験に対応する多粒子系モデルである.質点数2712,要素数5232である.ばね・質点系の運動方程式をたて,実験に対応した収納状態と回転数を初期条件として,Runge-Kutta法で数値積分を行うことにより,遠心力展開ダイナミクスの数値シミュレーションを行うことができる.展開中の膜面形状と展開率(展開中の半径/最大半径)の実験結果と数値シミュレーション結果の比較を図4, 5に示す.定性的に両者はよく一致するが,座屈強度や空気抵抗などのモデル化の効果により,定量的にもシミュレーション結果が大幅に改善されることが確認できた.実験と数値シミュレーションによる展開挙動の動画を図6に示す(IE以外ではうまく再生できないかもしれません).
  |
 |
|
| 図1. 四角形要素 | 図2. 三角形要素 | 図3. ばねの復元力特性 |
 |
 |
| 収納時 | 展開時および拡大図 |
| 図3. らせん折り膜面多粒子系モデル | |
 |
 |
| (a) 実験 | (b) 数値シミュレーション |
| 図4. 展開形状の比較 | |
 |
| 図5. 展開率の比較 |
| (a) 実験結果(固定カメラで撮影) | (b) シミュレーション結果(回転系で作成) |
| 図6. 展開挙動の動画(IE以外ではうまく再生できないかもしれません) | |
四角折り膜面の遠心力展開ダイナミクス
らせん折りと同様に,IKAROSで作用された四角折り膜面についても,圧縮剛性や折り目剛性などのモデルを改良し,小型実験モデルと実機サイズの遠心力展開のシミュレーションを行っている.
参考文献