回転円形膜面の平衡状態と振動モードに関する研究


概要

柔軟構造物の理論解析法の研究と遠心力で展開する膜面構造物の実現性の検討のため，分布荷重が作用する回転円形膜面の力学特性を解析と実験によって研究している． 既往の回転円形板（膜）の振動解析では，有限面外変形を表現するvon Karmanの非線形理論（Föpplの膜理論）を適用した研究が多数あるが，非常に薄い膜面の大変形に対する適用限界は不明確である．そこで，理論解析や実験，数値解析によって，回転円形膜の力学特性について検討している．

平衡状態

面外分布荷重（重力）下を受ける回転円形膜の平衡状態における面外変位を求めるため，膜の曲げ剛性を無視，変形前後の回転対称形状を仮定し，面外大変形を表現可能な回転対称シェルの膜理論を適用して理論解析を行った．面外荷重による面外変形に伴って，膜面の周方向に圧縮荷重が生じるが，曲げ剛性の微小な膜面は圧縮に耐えられずに容易に座屈する．そのため，計算上で圧縮荷重が負になるとゼロにする近似を行って，座屈を考慮した解析を行った．外周部の面外変位の解析結果を真空槽内での実験結果と比較した結果，面外変形が大きい場合においても解析の妥当性を確認した．実験で得られたいくつかの回転数における平衡形状の写真を図1に示す．面外変位の解析結果と実験結果の比較を図2に示す．

   
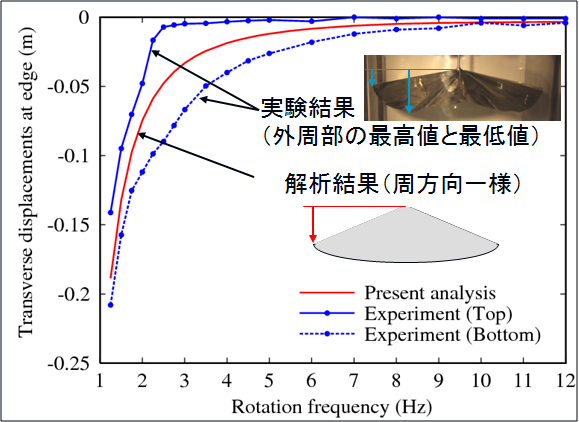 図1. 平衡形状 図2. 解析結果と実験結果の比較

微小振動モード

上記の解析で得られた平衡状態の周りの微小振動モードを求めるため，周方向モード形状は正弦波を仮定し，半径方向モード形状は数値解析によって求める理論解析と数値解析のハイブリッド的な手法を考案した．解析結果を多粒子系モデルの固有値解析結果や実験結果と比較検討し，理論解析と多粒子系モデルの固有値解析結果がほぼ一致することを確認した．解析で得られた振動モード形状を図3に示す．また真空チャンバ内の実験で自然発生した1つの振動モードについて解析結果が整合することを確認した．
その後さらに，円形膜面を回転させながら小型動電型加振機で加振する機構を製作し，強制振動実験を行った結果，2種類の共振点と種々の振動モードの計測に成功した．基本的なモードや共振点は解析結果と概ね整合したが，実験では振動時に膜にしわが発生し，最低次モードの共振点が解析結果より上昇する現象が見られた．

 
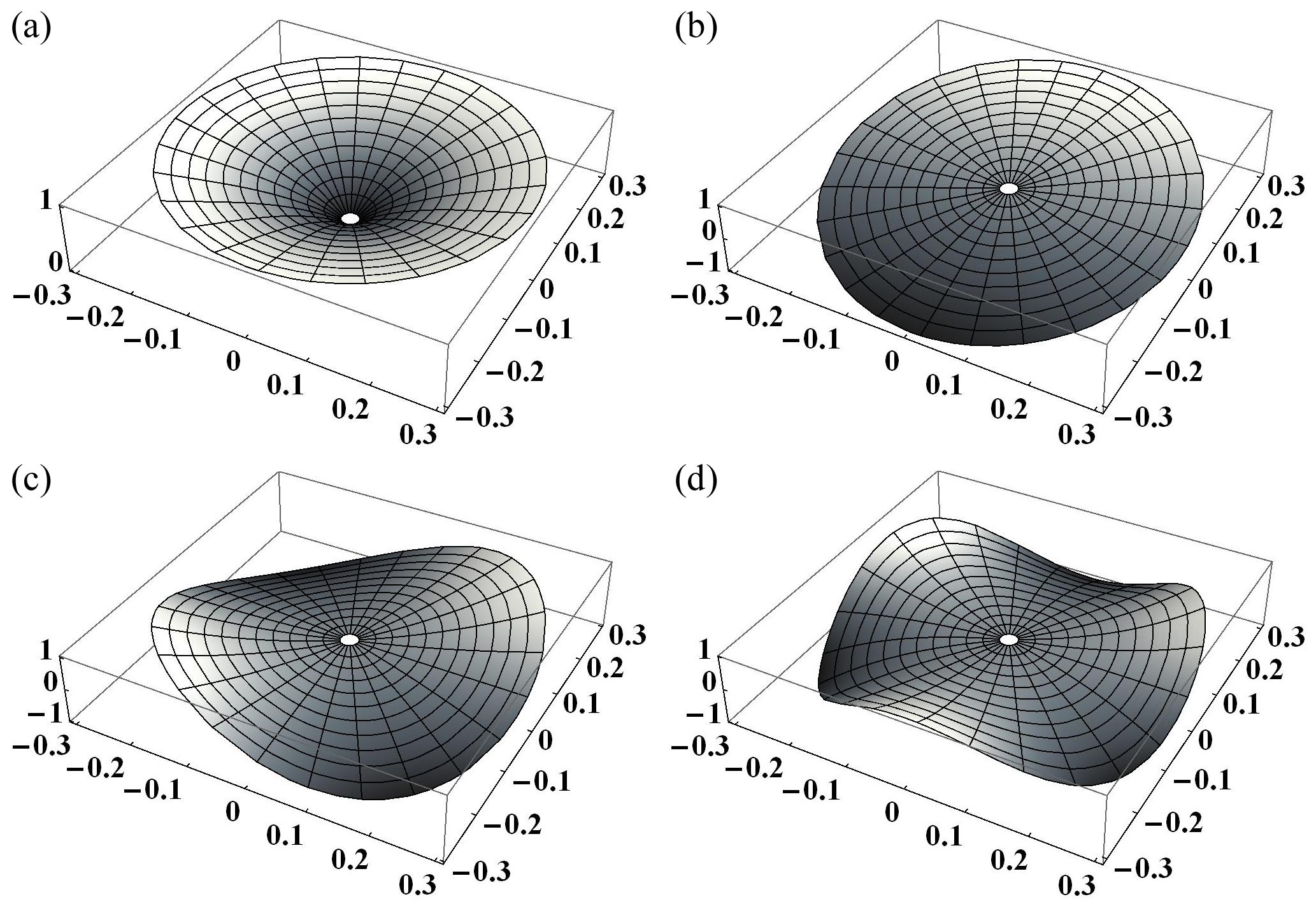 図3. 代表的な振動モード形状

参考文献

前にもどる